Descargas de libros y guías universitarias

Descargar guías de Tablas de Verdad

Es una herramienta desarrollada por Charles Peirce en los años 1880, siendo más popular el formato que Ludwig Wittgenstein desarrolló en su Tractatus lógicophilosophicus publicado en 1921. Se emplean en lógica para determinar los posibles valores de verdad de una expresión o proposición molecular. O si un esquema de inferencia, como argumento, es formalmente válido mostrando que efectivamente, es una tautología.

Una tabla de verdad es un arreglo rectangular que establece TODAS las posibles combinaciones de valores de verdad de las variables proposicionales (v.p.) de una forma proposicional (f.p.) y determina los valores correspondientes a esa forma proposicional para cada una de esas combinaciones, es decir, cada renglón será una interpretación posible para esa forma proposicional a partir de las diferentes combinaciones de valores de verdad para las VP que la compongan.

Una vez que conocemos el valor de verdad que se le asigna a cada variable proposicional y tenemos presentes las definiciones de los conectivos resulta fácil determinar el valor de verdad que le corresponde a la fórmula completa.

El procedimiento de determinación requiere ir por pasos, estableciéndolos valores correspondientes a los diferentes niveles (indicados por los signos de agrupación) hasta alcanzar el nivel de la forma proposicional completa. Así obtenemos una tabla de verdad para la forma proposicional.

El criterio para determinar cuántas filas posibles tiene una forma proposicional de-pende del número de variables proposicionales distintas que aparezcan en ella. Dado que según el Principio de Bivalencia que rige la Lógica Clásica una variable proposicional sólo puede tener dos valores de verdad (a saber, V o F) para una fórmula que contenga n variables proposicionales, el número de filas viene dado por la expresión 2ⁿ. Así la tabla de verdad de una fórmula que tenga 2 variables proposicionales tendrá 22 = 4 filas, una que tenga 3 variables, tendrá 23 = 8, una que tenga 4 variables 24 = 16 y así sucesivamente.

Algunos autores por ejemplo agrupan los conectivos que se utilizan sobre las proposiciones, en el cálculo proposicional en dos agrupaciones

Monódico (monario): envuelve solamente una expresión de la declaración

La negación simbolizada por “~” se lee NO, también se utiliza el símbolo “¬”

Diádico (binario): envuelve dos proposiciones.

El conectivo conjunción es simbolizado por "^" y se lee "y"

El conectivo disyunción inclusiva es simbolizado por "v" y se lee "o"

El conectivo condicional es simbolizado por “→” y se lee "Sí... entonces"

El conectivo bicondicional es simbolizado por "↔" y se lee "Sí y solo sí"¨

Conectivo Símbolo Se lee

Negación ~ No

Conjunción ^ Y

Disyunción v O

Condicional → Si,…entonces

Bicondicional ↔ Sí y sólo sí

Negación: Al negar una expresión obtenemos el valor opuesto de la original

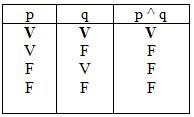
Conjunción: la conjunción de dos proposiciones cualquiera indica la verdad simultánea de ambas, la proposición compuesta resultante es verdadera si efectivamente ambas son verdaderas, (es como si al abrir una cuenta corriente apareciera una "y" en el lugar de las firmas; ambas personas tendrían que firmar para que el cheque tuviese validez), con cualquier otra posibilidad la conjunción será falsa.

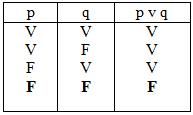
Disyunción: la disyunción tiene la función de enlazar dos proposiciones, indicando que al menos una de ellas es verdadera (aunque pueden serlo ambas también); con el ejemplo de la cuenta corriente si al abrir la cuenta se colocara un "y/o" cualquiera de las firmas haría válido al cheque, al igual que ambas. Por tanto la disyunción será verdadera si al menos una de las alternativas es verdadera (y por supuesto cuando las dos lo sean). Será falsa sólo cuando las dos proposiciones sean falsas.

Condicional: Al relacionarse dos proposiciones con este conectivo es muy importante distinguir la variable proposicional que queda a la izquierda (a la que se le llama antecedente o condición), de la que queda a la derecha (que se llama consecuente o consecuencia). El sentido de este conectivo es señalar, que si la proposición antecedente es verdadera, también lo es la proposición consecuente, de aquí que una proposición compuesta en la que el conectivo es condicional, será falsa si siendo verdadero el antecedente, es falso el consecuente. La proposición será verdadera en cualquier otro caso.

Bicondicional: Esta expresión es un conectivo lógico que al relacionar dos proposiciones indica que el valor de verdad de ambas es el mismo, ya sea verdadero o falso. Así, p↔q es una forma proposicional que significa que si p es verdadera, entonces q también es verdadera y si q es verdadera, entonces p también es verdadera. En realidad el conectivo bicondicional es la conjunción (^) de dos formas proposicionales condicionales (si...entonces), es decir, la forma proposicional p↔q tiene el mismo significado que la forma proposicional (p→q)  (q→p). En este conectivo la regla a utilizar es la siguiente, la forma proposicional es verdadera siempre y cuando las dos proposiciones tengan el mismo valor de verdad, si los valores de verdad son diferentes el bicondicional es falso.

Una manera de resumir toda la información en la siguiente tabla.

P	Q	˄	˅	→	↔	NOTAS
V	V	V	V	V	V	N° de filas
V	F	F	V	F	F	2²= 4 ; 2³= 8...
F	V	F	V	V	F	4/2= 2 ; 2/2= 1...
F	F	F	F	V	V
		Y es (V) cuando p y q son (V)	O es (F) cuando p y q son (F)	Entonces es (F) cuando de una (V) llegue a una (F)	Si y solo si es (V) cuando las dos tienen el mismo valor de (V)	2ⁿ= n.v Número de variables n.v/2 = cantidad de (V) y (F)

Descargar Guía de Ejercicios. Tablas de Verdad. UC
Descargar Guía de Ejercicios Resueltos. Tablas de Verdad. UC

Descargas de libros y guías universitarias

viernes, 26 de agosto de 2016

Descargar libros de Química.

viernes, 19 de agosto de 2016

Descargar Guías de Sociología / Sociología de las organizaciones. UC.

Descargar guías de ejercicios Introducción a la Matemática / Logica. UC.

Descargar guías de Tablas de Verdad